Burnside normal p-complement theorem. Let p be a prime number, G a finite group, and P a p-Sylow subgroup of G. If P is central in its normalizer then it admits a normal complement in G.
[See
here]
Thompson's thesis result. Let G be a finite group admitting a fixed-point-free automorphism of prime order. Then G is nilpotent.
[See
here]
I found
here a nice proof of the following result using the previous two. I will write it down with some details.
Herstein Theorem. Let the finite group G admit an abelian maximal subgroup. then G is solvable.
Proof. Let M be an abelian maximal subgroup of G. Since the normal core
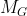
of M in G is abelian, we are reduced to show that
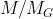
is solvable, hence we may assume that
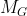
is trivial. Let p be a prime divisor of
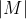
, and let P be a Sylow p-subgroup of G containing a Sylow p-subgroup of M. Suppose
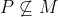
. Since P is a p-group, there exists
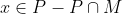
which normalizes
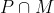
. Since M is abelian and maximal in G,
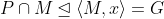
, contradicting
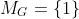
. Therefore
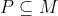
. This proves that M is a Hall subgroup of G, i.e.
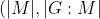=1)
. By Burnside normal p-complement theorem, every Sylow p-subgroup of M admits a normal complement in G, and the intersection of these normal complements gives a normal complement N of M in G. Let
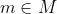
be an element of prime order. Since M centralizes m, it normalizes
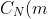)
, thus
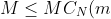 \leq G)
. If
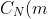 \neq \{1\})
then the maximality of M implies that
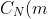=N)
, i.e.
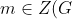)
, contradicting
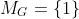
. Therefore
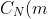=\{1\})
, so m induces a fixed-point-free automorphism of N of prime order, and by Thompson's result N is nilpotent. Since
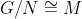
is abelian, this implies that G is solvable.